Cara Menghitung Luas Permukaan Prisma

KOMPAS.com - Prisma adalah bangun ruang tiga dimensi yang terdiri dari dua bangun datar yang memiliki bentuk yang sama persis dan saling berhadapan yang disebut sebagai alas.
Dilansir dari Splash Learn, alas pada prisma dapat berupa bentuk segitiga, persegi, persegi panjang atau bentuk lain yang memiliki beberapa sisi.
Jika prisma dipotong oleh garis lurus dan dibagi sama besar, maka akan dihasilkan bentuk penampangnya. Penampang prisma yang sejajar dengan alas prisma sama dengan alasnya.
Alas prisma dapat berupa bentuk simetris sama sisi ataupun asimetris, berdasarkan bentuk alasnya prisma dapat dibedakan menjadi prisma beraturan dan prisma tidak beraturan.
Jumlah sisi prisma adalah n+2, misalnya prisma segitiga berarti 3+2= 5, jadi prisma segitga memiliki 5 sisi.
Baca juga: Pembiasan Cahaya pada Prisma
- Rumus Prisma
| Nama | Rumus |
| Volume (V) | L = Luas alas (La) × tinggi |
| Tinggi (t), jika diketahui V | t = V ÷ Luas alas |
| Luas Permukaan (L) | L = t × (Keliling alas) + (2 × La) |
- Contoh soal prisma segitiga:
Jika diketahui sebuah prisma segitiga memiliki tinggi 12 cm, panjang sisi alas segitiga 6 cm, 8 cm, dan 10 cm. Maka cara menghitung volumenya adalah:
((alas × tinggi) : 2) × tinggi
((6 × 8) : 2) × 12 = 288 cm³
- Contoh prisma persegi panjang:
Jika sebuah prisma persegi panjang memiliki ukuran panjang 10 cm, lebar 6 cm dan tinggi 4 cm maka volumenya adalah:
V = (p × l) × t
= (10 × 6) × 4
= 240 cm³
Luas alas prisma yang dihitung adalah jumlah dari semua permukaannya. Rumus untuk mencari luas permukaan prisma tergantung pada bentuk alasnya.
- Contoh prisma segitiga:
Sebuah prisma segitiga memiliki tinggi 7 cm dan panjang sisi alas 5 cm, 4 cm, dan 3 cm. Maka cara menghitung luas permukaannya adalah:
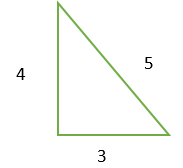 Alas prisma segitiga
Alas prisma segitiga
a1 = 5 cm
a2 = 3 cm
a3 = 4 cm
t = 7 cm
Karena alasnya berbentuk segitiga maka pertama-tama dicari dulu luas segitiganya dengan menggunakan rumus:
La = 1/2 × a × t
=1/2 × 3 × 4
= 6 cm²
Kemudian dapat dihitung luas permukaan:
L = t × (a1 + a2 + a3) + (2 × La)
= 7 × (5 + 3 +4 ) + (2 × 6)
= 84 × 12
= 96 cm²
- Contoh prisma persegi panjang:
Sebuah prisma persegi memiliki ukuran panjang 20 cm, lebar 12 cm, dan tinggi 10 cm. Karena alasnya berbentuk persegi panjang maka pertama-tama dicari dulu keliling persegi panjangnya dengan menggunakan rumus:
L = 2 × (p ×l + p ×t + l × t)
= 2 × (20 ×12 + 20 ×10 + 12× 10)
= 2 × 560
= 1.120 cm²