Persamaan Linier Kuadrat, Jawaban Soal TVRI SMA 4 Agustus 2020

KOMPAS.com - Program Belajar dari Rumah kembali tayang di TVRI, Selasa, 4 Agustus 2020.

Dalam tayangan hari ini, siswa SMA dan SMK belajar mengenai sistem persamaan linier kuadrat.

Di akhir segmen, ada pertanyaan yang bisa dikerjakan untuk berlatih. Simak pembahasan ketiga pertanyaan!

Soal: Solusi dari sistem persamaan linier y = 2x-5 dan kuadrat y = x²-3x+1 adalah…

Jawaban: Langkah pertama, substitusikan kedua persamaan

y = 2x-5
y = x²-3x+1

2x-5 = x²-3x+1

Kemudian, buat menjadi persamaan kuadrat, jadikan satu ruas

x²-3x+1-2x+5 = 0
x²-5x+6 = 0

Faktorkan persamaan. Cari dua bilangan yang apabila dikalikan nilainya 6, dan jika dijumlahkan nilainya -5. Kedua bilangan itu adalah -2 dan -3.

x²-5x+6 = 0
(x-2) (x-3) = 0
x = 2 dan x = 3

Setelah mendapat nilai x, masukkan ke dalam salah satu persamaan. Pilih persamaan linier yang lebih mudah untuk mencari nilai y.

• x = 2

y = 2x-5
y = 2.(2)-5
y = 4-5
y = -1
Solusinya adalah (2, -1)

• x = 3

y = 2x-5
y = 2.(3)-5
y = 6-5
y = 1
Solusinya adalah (3, 1)

Dengan demikian, solusi dari sistem persamaan linier y=2x-5 dan kuadrat y=x²-3x+1 adalah (2, -1) dan (3, 1).

Soal: Terdapat dua buah titik potong antara garis x+2y=7 dan lingkaran x²+y²=10. Tentukanlah koordinat kedua titik potong tersebut.

Jawaban: Langkah pertama, substitusikan x+2y=7 ke dalam x²+y²=10!

x²+y² = 10
x²= 10-y²

x+2y = 7
x = 7-2y

(7-2y)² = 10-y²
(7-2y) (7-2y) = 10-y²
49-14y-14y+4y² = 10-y²
49-14y-14y+4y²-10+y² = 0
49-28y+5y²-10 = 0
5y²-28y+39 = 0
(5y-13) (y-3)

y = 13/5 dan y = 3

Kemudian, untuk mencari dua buah titik potong (x1, y1) dan (x2, y2), tinggal masukkan nilai y yang telah kita dapatkan.

• x1 dengan y = 13/5

x = 7-2y
x = 7-2(13/5)
x = 35/5-26/5
x = 9/5

Koordinat pertama (x1, y1) adalah (9/5, 13/5)

• x2 dengan y = 3

x = 7-2y
x = 7-2(3)
x = 7-6
x = 1

Koordinat kedua (x2, y2) adalah (1, 3)

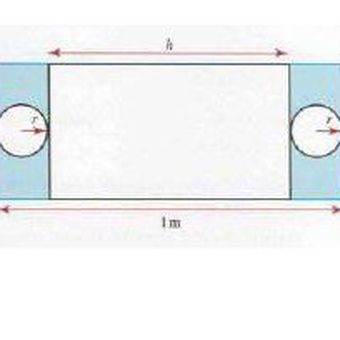jaring-jaring wadah tabung

1. Tuliskan sistem persamaan linier-kuadrat dalam r dan h
2. Hitunglah volume wadah tabung tersebut dalam cm³

Jawaban:

a. Diketahui:

Luas permukaan tabung = 1.400π cm²
Panjang lembar = 1 meter = 100 cm
Panjang persegi (tabung) = h = 100-4r
Lebar persegi panjang (tabung) = keliling lingkaran tabung = 2πr

1.400π = 2L lingkaran + L persegi panjang
1.400π = 2πr² + (panjang. lebar)
1.400π = 2πr² + ((100-4r). 2πr)
1.400π = 2πr² + (100-4r. 2πr)
1.400π = 2πr² + 200πr - 8πr²
1.400π = 200πr - 6πr² (coret pi di setiap ruas)
1.400 = 200r - 6r²
6r² - 200r +1400 = 0

b. Untuk mencari volume tabung, cari dulu nilai r dari persamaan yang telah kita dapatkan!

6r² - 200r +1400 = 0
(6r - 140) (r - 10)
r = 10 dan r = 140/6 atau 70/3

Masukkan nilai r ke dalam rumus volume tabung:

Vt = πr².t
Vt = π10².2π10
Vt = 2.000π²

Vt = πr².t
Vt = π70/3².2π70/3
Vt = 343.000/27π²

Dua jawaban volume tabung adalah 2.000π² cm³ dan 343.000/27π² cm³